概述
解决的问题
无修改的离线区间询问问题
对问题的要求
假设 $n$ 为下标范围,$m$ 为询问次数,若从 $[l, r]$ 的答案能够以某种方式(假设一次转移的复杂度为$\Theta(x)$)扩展到 $[l - 1, r], [l + 1, r], [l, r + 1], [l, r - 1]$的答案,那么所有询问可以使用莫队算法在 $\Theta((n + m) \sqrt{n} \cdot x)$ 的时间内求出
实现
简易版本
流程
- 离线后排序(左端点 $l$ 为第一关键字,右端点 $r$ 为第二关键字)
- 设置初始位置:$l = 1, r = 0, now = 0 (now为当前答案)$
- 顺序处理每个询问
代码
注:此代码以统计区间不同数字个数为例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| struct Query {
int l, r;
int id, ans;
};
int n, m;
int a[MAXN];
Query q[MAXQ];
int cnt[MAXN];
int l, r, ans;
bool cmpRG(const Query &_a, const Query &_b) { // 左端点为第一关键字,右端点为第二关键字
if(_a.l != _b.l) {
return _a.l < _b.l;
} else {
return _a.r < _b.r;
}
}
bool cmpID(const Query &_a, const Query &_b) { // id
return _a.id < _b.id;
}
void add(int x) { // 向区间添加元素,更新当前答案
cnt[a[x]]++;
if(cnt[a[x]] == 1) {
ans++;
}
}
void del(int x) { // 从区间删除元素,更新答案
cnt[a[x]]--;
if(cnt[a[x]] == 0) {
ans--;
}
}
int main() {
// Code here...
for(int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r;
q[i].id = i;
}
sort(q + 1, q + m + 1, cmpRG); // 对区间排序
l = 1; // 初始位置
r = 0;
ans = 0;
for(int i = 1; i <= m; i++) {
while(r > q[i].r) { // 移动到新区间
del(r--);
}
while(r < q[i].r) {
add(++r);
}
while(l > q[i].l) {
add(--l);
}
while(l < q[i].l) {
del(l++);
}
q[i].ans = ans;
}
sort(q + 1, q + m + 1, cmpID); // 恢复原顺序
// Code here...
}
|
优化
过程
可以发现,在最劣的情况下,比如询问的区间为 $[1, 1], [1, 50], [1, 100], [2, 2], [2, 50], [2, 100], [3, 3], [3, 50], [3, 100]$ 时,左端点只会移动 $3$ 次,但是右端点会移动大约 $300$ 次
但是,如果对其按如下方式排序,移动次数就会大大降低
$$
[1, 1], [2, 2], [3, 3], [1, 50], [2, 50], [3, 50], [1, 100], [2, 100], [3, 100]
$$
此时左端点大约会移动 $10$ 次,而右端点则会移动 $100$ 次
这只是一个极端情况,对于普遍的情况,莫涛大神则提出了一种基于分块的方法:
- 将下标范围 $[1, n]$ 分为 $\sqrt{n}$ 块($[1, \sqrt{n}], [\sqrt{n} + 1, 2\sqrt{n}] \dots$)
- 以区间左端点所在的块的编号为第一关键字,以右端点为第二关键字对所有询问区间排序
- 设置初始位置并顺序处理每个询问(同上)
这样,对于每一个块中的询问(此处询问所在的块即指询问左端点所在的块),右端点的移动范围都是 $n$(因为同一块内询问右端点有序,最多只会从下标 $1$ 移到下标 $n$),所以右端点移动的总复杂度为 $\Theta(n\sqrt{n})$(总共有 $\sqrt{n}$ 个块);而对于左端点,如果在块内移动,那么范围就是 $\sqrt{n}$,如果在块间移动,那么范围至多也不超过 $\Theta(2\sqrt{n})$(移动到下一个区间),所以左端点移动的总复杂度为 $\Theta(m\sqrt{n})$(每次移动都是 $\Theta{\sqrt{n}}$)
所以,算法总复杂度为 $\Theta((n + m) \sqrt{n})$,如果算上每次移动的复杂度为 $\Theta(x)$,则总复杂度为 $\Theta((n + m) \sqrt{n} \cdot x)$
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| struct Query {
int l, r;
int id, ans;
};
int n, m;
int a[MAXN];
Query q[MAXQ];
int cnt[MAXN];
int l, r, ans;
int block;
bool cmpRG(const Query &_a, const Query &_b) { // 左端点为第一关键字,右端点为第二关键字
if(_a.l / block != _b.l / block) {
return _a.l < _b.l;
} else {
return _a.r < _b.r;
}
}
bool cmpID(const Query &_a, const Query &_b) { // id
return _a.id < _b.id;
}
void add(int x) { // 向区间添加元素,更新当前答案
cnt[a[x]]++;
if(cnt[a[x]] == 1) {
ans++;
}
}
void del(int x) { // 从区间删除元素,更新答案
cnt[a[x]]--;
if(cnt[a[x]] == 0) {
ans--;
}
}
int main() {
// Code here...
block = sqrt(n);
for(int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r;
q[i].id = i;
}
sort(q + 1, q + m + 1, cmpRG); // 对区间排序
l = 1; // 初始位置
r = 0;
ans = 0;
for(int i = 1; i <= m; i++) {
while(r > q[i].r) { // 移动到新区间
del(r--);
}
while(r < q[i].r) {
add(++r);
}
while(l > q[i].l) {
add(--l);
}
while(l < q[i].l) {
del(l++);
}
q[i].ans = ans;
}
sort(q + 1, q + m + 1, cmpID); // 恢复原顺序
// Code here...
}
|
再优化(蛇形移动)
可以发现,每次从一个块前往下一个块的时候,左端点常常会移动很远,此时,我们可以利用蛇形移动来优化。
我们先将左端点和右端点在坐标系中形象地表示出来:
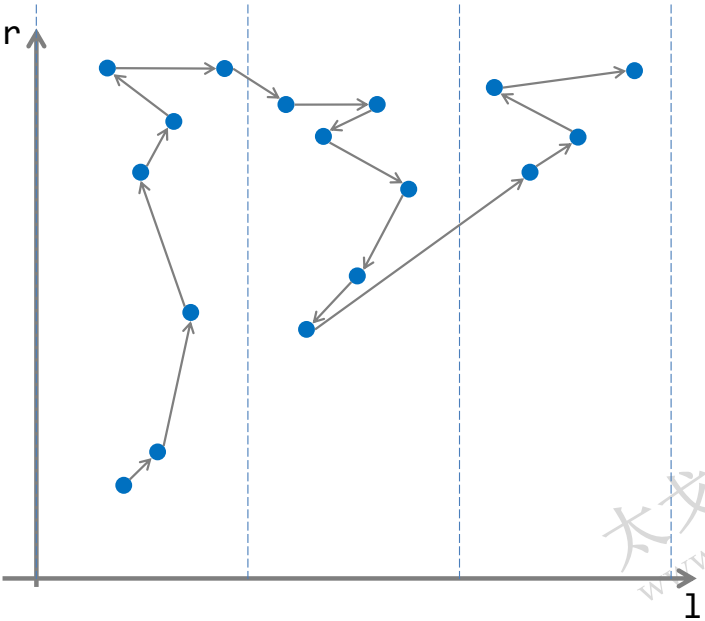
所谓蛇形移动,就是对于奇数块和偶数块在块内采用相反的方向按右端点排序。这样,每次解决完一个块时,我们不必使左端点回到头部,所以可以节省部分时间。
当然,这种方法通常是常数级优化。
具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| struct Query {
int l, r;
int lid; // 左端点所在的块的编号
int id, ans;
};
int n, m;
int a[MAXN];
Query q[MAXQ];
int cnt[MAXN];
int l, r, ans;
int block;
bool cmpRG(const Query &_a, const Query &_b) { // 左端点为第一关键字,右端点为第二关键字
if(_a.lid != _b.lid) {
return _a.lid < _b.lid;
} else {
if(_a.lid % 2) { // 奇数块
return _a.r < _b.r; // 升序排列
} else { // 偶数块
return _a.r > _b.r; // 降序排列
}
}
}
bool cmpID(const Query &_a, const Query &_b) { // id
return _a.id < _b.id;
}
void add(int x) { // 向区间添加元素,更新当前答案
cnt[a[x]]++;
if(cnt[a[x]] == 1) {
ans++;
}
}
void del(int x) { // 从区间删除元素,更新答案
cnt[a[x]]--;
if(cnt[a[x]] == 0) {
ans--;
}
}
int main() {
// Code here...
block = sqrt(n);
for(int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r;
q[i].lid = q[i].l / block;
q[i].id = i;
}
sort(q + 1, q + m + 1, cmpRG); // 对区间排序
l = 1; // 初始位置
r = 0;
ans = 0;
for(int i = 1; i <= m; i++) {
while(r > q[i].r) { // 移动到新区间
del(r--);
}
while(r < q[i].r) {
add(++r);
}
while(l > q[i].l) {
add(--l);
}
while(l < q[i].l) {
del(l++);
}
q[i].ans = ans;
}
sort(q + 1, q + m + 1, cmpID); // 恢复原顺序
// Code here...
}
|
