分析
我们不妨把这些座位看作是一张图中的节点,把每个人的诉求作为一条边(由【原座位】指向【想去的座位】)
比如,对于样例#1,我们就可以得到这样一张图:
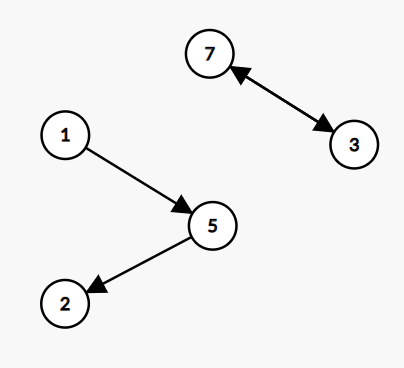
显然,我们有可能会得到多个连通图(比如上面这张)
因为每个座位上的人都只有一个想去的座位,所以每个点的出度就是 $0$(可能只有其他的点指向它) 或 $1$,整每个连通图的边数就是 $n$ (点的个数)或者 $n - 1$ 个
当边数等于 $n$ 时,显然这是一个环或者一棵基环树(定义见这里)
我们以这组数据举例:
1
2
3
4
5
6
7
8
| 7
1 2
2 4
3 2
4 1
5 3
6 3
7 6
|
手画一下复制到Graph Editor,可以得到这张图:
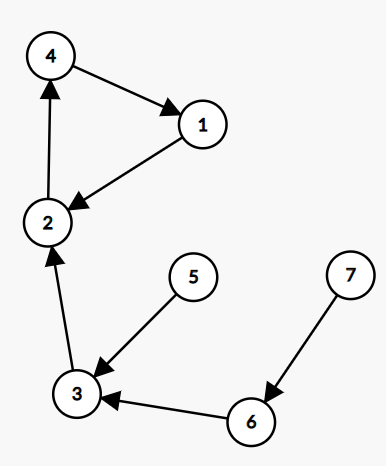
试着移动每一个点,容易发现:移动r任意环外点(比如这里的 $3$、$5$、$6$、$7$),环上的点肯定就没位置了。
证明(废话) :点 $2$ 唯一的一条出边已经用在环上了,所以 $2$ 和任意环外点之间的边一定是指向 $2$ 的,以此类推,我们可以发现:$3$、$5$、$6$、$7$ 对应的边都是指向 $2$ 的。于是,只要移动必定会移到 $2$ 的位置
于是我们就可以得到结论:如果这是一棵基环树或者一个环,那么它的答案为 $2$(环内的点移/不移,两种情况)
当边数等于 $n$ 时,显然这是一棵树
我们拿它举例:
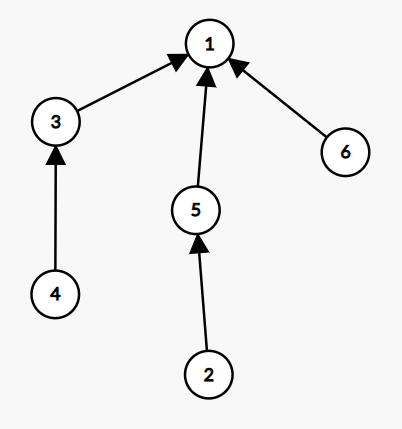
每个节点的出度都为 $1$ 或 $0$(只可能有一个点出度为 $0$,这个座位一开始就空着),所以我们可以将唯一的那个出度为 $0$ 的点(如这张图中的点 $0$)作为树根。
显然,我们移动任意一个点,都会导致一种确定且不重复的情况(它到根节点的链上的每一个点都往上移),所以其答案为 $n$,即点数
于是,最终的答案就是将每个连通图的答案乘起来。
HowTo
我们现在需要一种方法,可以判环、可以记录每个连通图的大小。
显然,并查集很合适。
每输入一个人的要求,我们就把这两个点所在的集合(连通图)合并(merge函数),同时记录集合大小(sz数组)。如果合并前这两个点已经在同一个集合中,那么,这一定是一个环(两点之间有不止一条路径),做一下标记。
最后,统计答案即可。
你以为结束了?
还有一个坑。。。
出现自环时,不能向上面那样考虑,因为这一个点移动后还在原来的位置,所以答案是 $1$(最终ans不变)
细节请看代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include <bits/stdc++.h>
using namespace std;
#define int long long // 好习惯:随时开long long
#define MAXN 200005
#define MOD 1000000007 // 记得取模
int n;
int fa[MAXN]; // 并查集 - 父节点
int sz[MAXN]; // 并查集 - 集合大小
bool ish[MAXN]; // is环(记录此集合是否有环)
bool iszh[MAXN]; // is自环
void init(int x) { // 并查集 - 初始化
for (int i = 1; i <= x; i++) {
fa[i] = i;
sz[i] = 1; // 初始大小都是1
}
}
int find(int x) { // 并查集 - 查找
if (fa[x] == x) {
return x;
} else {
return fa[x] = find(fa[x]);
}
}
void merge(int x, int y) { // 并查集 - 合并
int fx = find(x);
int fy = find(y);
if (fx == fy) { // 已经在同一个集合
return;
}
iszh[fy] |= iszh[fx]; // 合并自环信息
sz[fy] += sz[fx]; // 合并大小
fa[fx] = fy;
}
signed main() {
cin >> n;
init(n * 2); // 初始化
for (int i = 1; i <= n; i++) {
int a, b;
cin >> a >> b;
if (a == b) {
iszh[find(a)] = 1; // 标记当前集合含有自环
}
if (find(a) == find(b)) { // 已经在同一个集合了
ish[find(a)] = 1; // 标记当前集合含有环
}
merge(a, b); // 连接这两个座位
}
int ans = 1;
for (int i = 1; i <= n * 2; i++) {
if (find(i) == i) { // i是一个集合的代表
if (ish[i]) { // 含有环
if (iszh[i]) { // 自环,答案不变
continue;
}
ans *= 2;
ans %= MOD;
} else { // 不含有环
ans *= sz[i];
ans %= MOD;
}
}
}
cout << ans << endl;
}
|
AC


